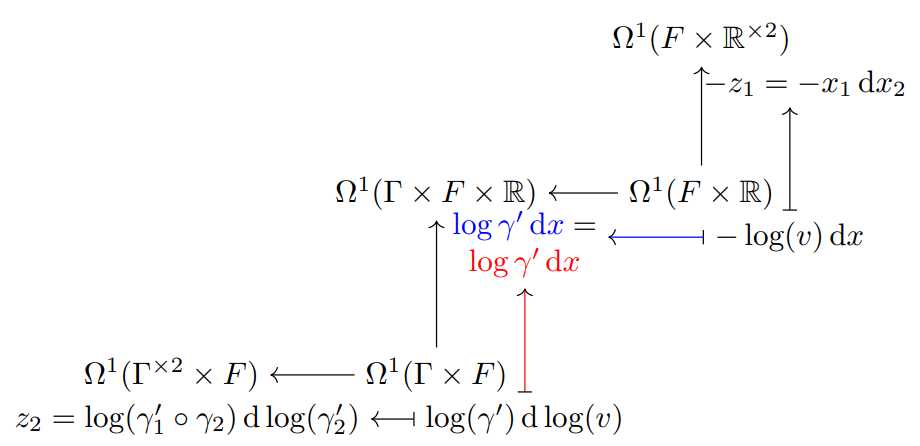Mathematics

I did my DPhil in Mathematics under the supervision of André Henriques at Oxford University. My research was focused on smooth higher algebra in low dimension.

Manifold Tensor Categories

In part of my thesis, I introduce Manifold tensor categories, a generalisation of fusion categories. They show up naturally in theoretical physics, in particular the study of Defects in Conformal Field Theories with central charge $c = 1 .$ I give a precise meaning to the idea of a tensor category with a manifold of simple objects, establish basic properties of the resulting notion, and construct explicit examples. I also prove a Smooth Dualisability Theorem. I further treat the case of an orbifold of simple objects, and term the resulting notion Orbifold tensor categories. Examples of such categories appear, for example, in the representation theory of virtually abelian groups (such as the wallpaper groups ).

The moduli space of simple objects of the Orbifold Tensor Category ${R e p}^{u} (Σ_{3} ⋉ ℤ^{2}),$ of unitary representations of the wallpaper group *p31m*. Its associated orbifold is the quotient of a torus by the action of $Σ_{3} .$

The centres of String 2-groups

I computed the centres of String 2-groups. The result of this computation is interesting: the centre recovers the corresponding invertible loop group representations. This is also Chapter 3 of my thesis.

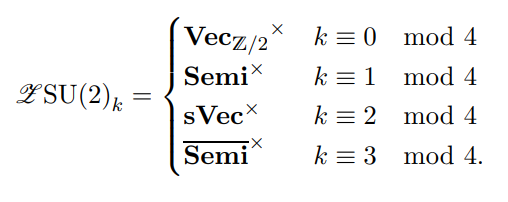
The centre of the String 2-group $S U (2)_{k}$ associated to the Lie group $S U (2)$ and level $k \in ℤ.$ It cycles through the Picard subgroups of four well-known braided fusion categories.

The Virasoro group and differential cohomology

Arun Debray, Yu Leon Liu, and I showed that the Virasoro group (a central extension of the group ${D i f f}^{+} (S^{1})$ of orientation preserving diffeomorphisms of the circle) may be obtained by transgressing a differential refinement of the first Pontryagin class. This answered a question of Freed-Hopkins.

A computation showing that the cocycles $z_{1}$ and $z_{2}$ are cohomologous. They both represent the Virasoro group extension with central charge -24.